_______
20090614—0629

There are many was to determine a parabola. However, I propose a simple solution with only knowing 2 points that lie on the parabola. It is important to note the following explanations may be completely wrong, or easily seen upon inspection of the parabola.

To find the slope of a parabola if not given, take the derivative of its equation. But upon close inspection the “x” value equals the slope and the “y” value is the integral of x. That is, “y” is equation of the parabola.

 

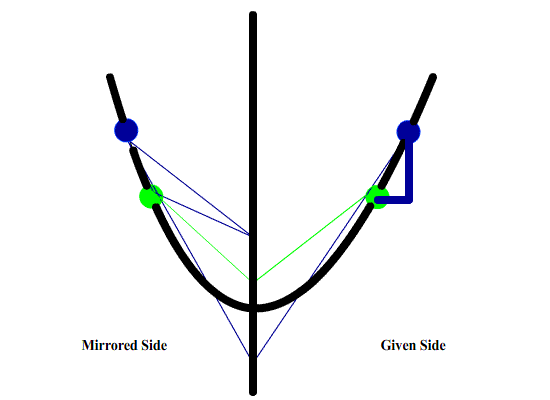
The first step is to find the line the focus will be found on. This is found by drawing the tangent or slope of each of the two points on the parabola. Next draw a mirrored representation of the parabola. For a parabola this is just the opposite side. The place where the tangent line of a point and its mirror cross is where a perpendicular line falls. This perpendicular line is the place on which the focus falls.

Two points were needed because one point would intersect infinitely many times. With two points the horizontal distance must be equal for both lines. Thus forming the perpendicular line the focus lies on.

Not to scale or proportion.

Now to find the focus, we make use of previous work of the mirrored ladder. We will be working in reverse. That is placing the point at the focus and solving the angles that make up the right angle. It sounds complex, but is rather simple in graphical form.

Click Here to View Mirrored Ladder

Referring to the Mirrored Ladder. We know the center value which is the distance as the distance to the perpendicular which the focus lies. We then can substitute any radius and use the know values to solve the equation much like the arc doorway problem.

 

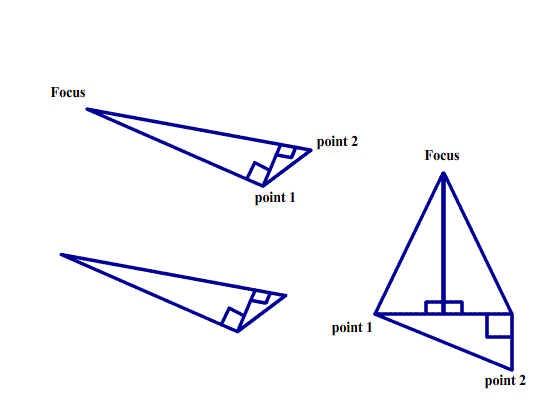
We also know the x and y distances because the coordinates are given.

I hope that you, the reader, can see it by the diagrams. This is just preliminary work. I will have to rewrite this simplifying and making it more understandable.

May the Creative Force be with You