| Here is the arc descibed by two isosceles triangles. As you can see a there are a bunch of other triangles in the drawing. It is fun just to tinker around and see what the other triangles do. Maybe your find the ones that best describe the arc and the triangles underneath. |  |
Another math topic though directly not related to the arc door problem is the ssin and scos. I originally came up with a simple description of the change in height and width of the cos and sin. The equation for the length “L” is hard to simplify when using equations. So if we could find a way to simplify the descriptions of the length. Or find and application for the ssin and scos we would have a little discovery and new tool to approach trigonometric problems. See figure below.
| These trigonometric descriptions (ssin and scos) may not be as useful as I had originally planed. It often occurs that there are simpler ways to describe the triangles and solve for them.But if you could find a way to descibe the change in the cos and sin like the Arc Doorway problem did you would have a very valuable discovery | 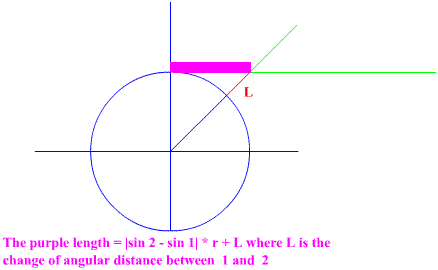 |