| Page 1 | Math Home | Ideas Home |
Intro: I am searching for new ways to use basic trigonometry and geometry to solve land navigational problems. (Perhaps even use the knowledge learned by the arc doorway problem.) Everything here is just based on the math I have learned. It is probably common knowledge with nothing newly discovered. Still it is interesting to think about. And the things we already know lead to the things that need uncovered. In land navigation the path finder is equipped with a compass and a map. By shooting angles and knowing the distance found by pace counter or the maps scale, he finds his way. To find position he simply finds two landmarks on his map. He shoots an azimuth or angle between one of the two points and his position. He then does the same with the second. Now he can use this angle and draw a line on the map from the landmark points. Where these two points cross is his position. The situation is different when cell phone towers have to locate the user’s phone. Here, since no angle is given, to find the user of the phone it would take 3 towers or points. The distance from the user to each tower is measured and where they intersect is the location of the user. Take a circle with a diameter of the distance and draw it around the position of the tower. With 3 circles the position is discovered, depending on the placement of the towers. But what if there was a way to find the location using distance with only 2 towers? In fact, there is an easy way to do this with only knowing the distance and direction between the two towers. Consider that the speed of the cell phones connect was taken by two towers. If you have two distances or circles around each tower, where they meet is the possible places for the cell phone user to be. The circles meet in two places, and it is possible that the location could be mirrored creating four possible locations. But since the distance between the two towers is given it eliminates two choices leaving two choices remaining. Finally the correct choice is found by knowing the direction between the two remaining points or towers. This leaves a triangle whose length of the sides are given and position is known. Now, the angles of the triangle can be solved by the law of cosines. Conclusion: This problem doesn’t really explain more than is already known. But it is an attempt to find little math cheats that can be used during land navigation. If you could discover something new that hasn’t been discovered yet, then you would find a method that pertains not only to land navigation but movement in general such as programming a video game characters movement on the computer. I know that the methods in the field of navigation have been exhausted, but the intention is not to reinvent the wheel. The intention is to steer the wheel in a different direction. In other words, the attempt is to apply all the math knowledge that we have learned.
|
Figure 1 shows one possibility of the cell users position. Figure 2 shows the other possible mirrored position. Once direction between the towers is given it eliminates the second possibility. |
|
figure 1
|
| .......notes | Page 1 | Math Home | Ideas Home |
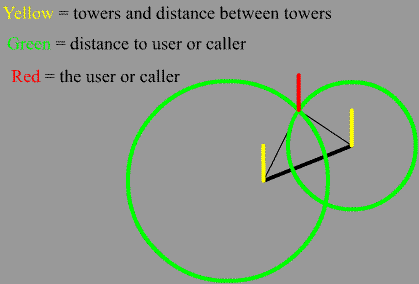
 figure2
figure2