| Page 1 | Math Home | Ideas Home |
Circle Key
|
Even though the parabola of a second degree polynomial equation may lie in negative (or imaginary) numbers, the parabola itself may still be measured using relative coordinates. In other words no matter where the parabola lies on the coordinate plane, the measured values of the parabola itself are still useful. The goal of this problem is to find a circular that encompasses a segment (and a line perpendicular to that segment). (Yes, it is the “arched doorway problem revisited”.) But what would be an application of this problem? It is another way of solving circular arcs and may lead to a better way to describe curves. But what I am looking for is an alternative to the Quadratic Equation. Finding a alternative to the Quadratic equation may seem too difficult, but this problem is a place to start. Another application of knowing what radius will encompass what line segment is a possible method of encryption. Matrices are often used for encryption. Matrices explain linear equations. The question is what if we had a way to better describe polynomial equations?
|
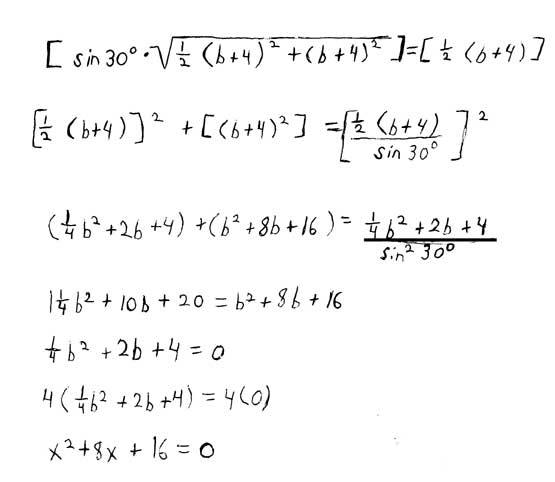
Now lets explore where these equations come from. Then we will see what they can do.
|
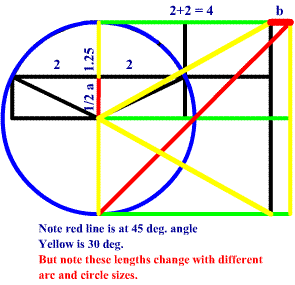
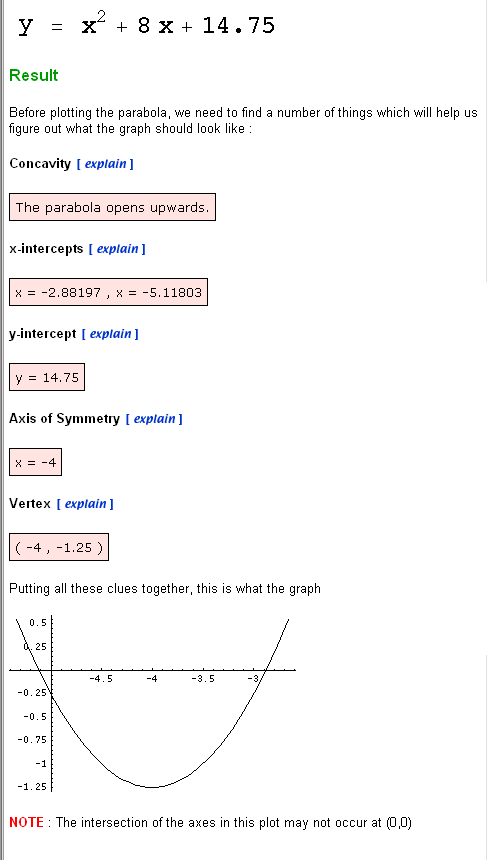
The equation originates as a square above and inscribed circle. The length of the square is equal to the radius of a circle. Here b + 4 equals a + 2.5 . We could try solving the sides by substitution but there is no easy (if any) way to isolate one of the variables (a or b). So that is the problem. We have to find at least 2 ways to describe b (or possibly a) so that we can get a real number value for b from those equations. And we will do it using elementary mathematics. Well a square is a special polygon where the length equals the width. So in this example b + 4 is equal to a + 2.5 . So relying on basic understanding of the Pythagorean Theorem there is a hunch that it is possible to solve for a or b. So Sqrt( (a +2.5)^2 + (b + 4)^2 = unknown. So the equation appears to go nowhere. But if since (a + 2.5) equals (b +4) we can substitute the values. So (b+4)^2 + (b+4)^2 = unknown. So in order to find another equation that describes b in a different way (a different way to achieve the same value), we must rely on the only other thing at our inventory. That is the trigonometric functions: sine, cosine, tangent, etc. It helps if we use our known special angles: 30, 45, 60 degrees respectively. If we were to draw a 30 degree angle from half the length of the length, this 30 degree angle would end at the top of the square since the sin 30 = 0.5 . Now we have just the observations we need to make use of the Pythagorean Theorem. The above equations could have been simplified in less steps, but the sin 30 shows where the values come from. The equation is actually very simple: b^2 + 8b + 16 = 0
|

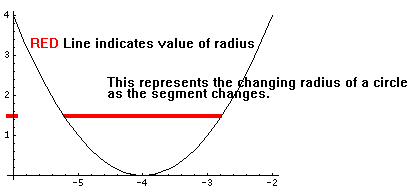
So we have the equation what we do with it. We have to solve for the parabola’s x and y values by using the Quadratic Equation. For example the example we have been using (the “Arch Doorway” problem), we would use the given length of the segment (the y value) and just plug it into the equation. For an easy starting point you could just plot the graph of the parabola. Then you take the y value as the value of the line segment (1.25 in the arch door ex.) and measure the x length span of the parabola. The radius of the desired circle equals the space in between the sides of the parabola. So the difference of the second x value minus the left x value equals the radius. This is the radius of the circle that would encompass the segment.
|
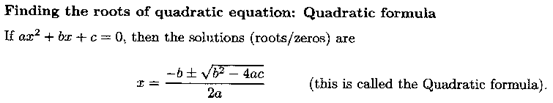
| the following graphics were produced using a quadratic calculator found at: |

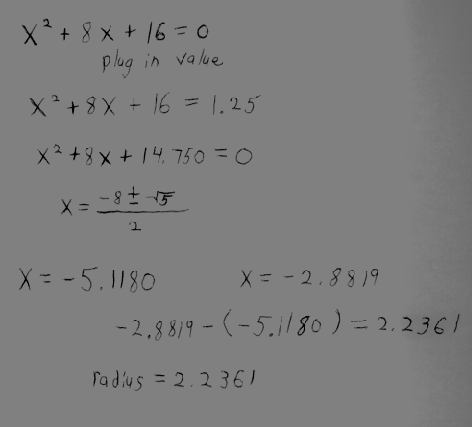

|
|

| The research into this problem is only beginning. This
is just a rough draft it needs some tweaking. Be sure to check out the
other math problem on the site. Many of them relate to this description.
But until I finish documenting this problem... May the Creative Force
be with You |
| Page 1 | Math Home | Ideas Home |