_______
20090913-0928
Theory
A series in Prime numbers, if one exist, should be able to be found on a parabola. The parabola should have its apex (the distance from the vertex of the parabola to a point on the parabola) equal to a Prime number for every Pi arc length along the graph of the curve.
This sounds simple enough until it comes time to find the equation of the parabola. Also note, (however confusing), that previously we were trying to solve a logarithmic spiral with a change in Prime number in series every Pi radians that equals an arc length, the actually curve along the graph, of the Prime number. If we were to switch the values of the apex from [k * Pi] every Prime number along the arc length then in theory, if the original logarithmic spiral and parabola we found were correct, they should be proven to work by the new approach. Also, it would make it easier since we already solved an equation for those graphs.
But here we will assume the original work to be incorrect, to solve the problem a different way and hopefully prove and find a series of Prime numbers.
Attempted Solution
Given:
1) Prime numbers occur every [k * Pi] exact arc length along the graph of the parabola.
2) Apex (the line from the vertex to a value on the parabola) is tested at least two Prime number. values
3) Distance of the apex for at least two Prime numbers. That is from the vertex to a value on the parabola. (It is important to note we do not know the values on the parabola yet. We know only the distance from the vertex. This is a challenge though not as difficult as it seems will be dealt with first.)
Work
First we will choose 3 Prime numbers. We will start with 3 because 2 is the only even Prime number and may skew calculations.
Prime number—number of Prime number in series of Prime numbers
3— [2 - 1] or 1
991— [167 - 1] or 166
3571— [500-1] or 499
Now, take a look at this parabola + focus + directrix excerpt from Wikipedia.org . I only know of one way to solve a parabola where only the distance from the vertex to values on the parabola is known. And that is geometric construction. Look at this picture before continuing to read. It is important.
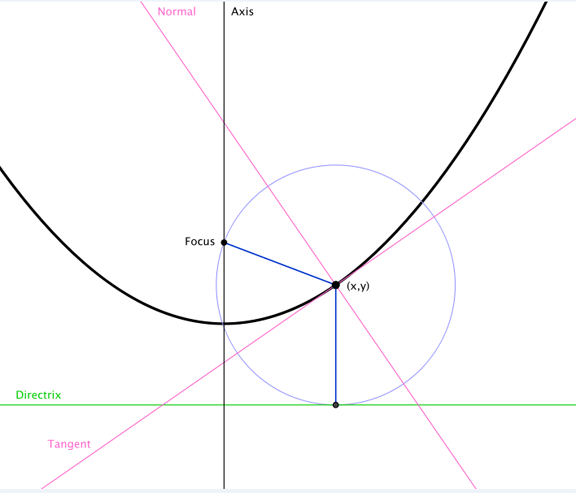
Geometric Construction
For the geometric construction choose an arbitrary point for the parabola’s vertex. From here draw a line horizontally and another long line vertically. We know that the focus lies on the vertical line above our arbitrary point (the vertex). By looking at the properties of the Wikipedia parabola drawing we know see with a few arcs of a compass we can find the focus, the vertex, and the unknown values on the parabola.
Now the arcs. Draw an arc with radius of the Prime number (for are values we chose 3) using the vertex (arbitrary point (for now)). Again from the vertex draw an arc double the previous radius (which would be 6) that crosses the long horizontal line. From this new point, where the arc crosses the long horizontal line, take the original radius (3) and draw an arc that intersects the first arc length made (the 3 radius arc). This is the place on the parabola where a apex, which is equal to a Prime number, connects to the value on the parabola.
To find the focus from the new point on the parabola just found, draw an arc with the original arc length (3 in our chosen value). The place where this arc crosses or intersects the vertical line above the vertex is the focus.
From the value on the parabola, draw a perpendicular line with the Prime number (3) as the length. Where this line ends is the directrix.
Next Steps
We now have the basic knowledge to place values into a parabolic equation. Here is one from Wikipedia.org .
![]()
Once we have the parabola’s equation we can then test to see if the theory works by finding the length of arc that occurs on the parabola when the apex equals a Prime number. This should occur every Pi arc length on the parabola.
The equation for arc length can be found at Paul’s Online Notes.
I will finish the write up soon. A need to verify the substitution rule for integrals. But in the mean time you may test it on your own. I know it seems to simple to work. But I still believe this may help reveal a pattern among Prime numbers.
Too be continued....
References
Wikipedia.org
http://en.wikipedia.org/wiki/Parabola
Paul’s Online Notes
http://tutorial.math.lamar.edu/Classes/CalcII/ArcLength.aspx