_______
20100605
So it has been said that you cannot divide vectors. Sure you can, the only problem is usually there is infinite possibilities.
Well I’m going to propose there is a useful, unique solution that can be found. If we know vectors A and C we can divide C by A. But to eliminate infinite possibilities we will solve for one specific case. That special case is where vector A is a segment on a circle with radius equal to vector C.
This solution relies on the Ssine and Scosine which has been discussed many times and is in the math section of constructorscorner.net
Basically the Scosine states:
L = the length from the radius to a perpendicular project from the radius at a different angle
So that,
L = [(|cos(theta1)| - (|cos(theta2)| / cos(theta2] * r
_______
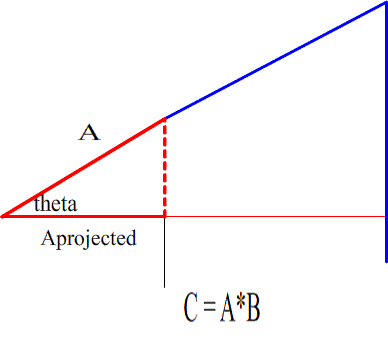
To find angle theta (between the A and C vectors, some minor calculations must be done. Take the scalar C divided by scalar Aprojected to get the scalar of B.
To get the angle between vector A and vector B, take the length of C (The length of C is the scalar of vector A project on vector B * vector B.) and find the vector where:
[Aprojected / sin(theta)] + L = C
_______
I believe this is a useful value of vector C / A because we are using a circle of radius C. This radius of C is the length of the scalar A * B.
Of course it is important to note that this is just a theory which needs proved and tested. This was the same reasoning behind finding the sides of a triangle knowing only 2 sides. Yes it is considered impossible because of the infinite possibilities, but what if there is a special case that when you use the special case you find some useful data among the infinite possibilities?
References: “Engineering Mechanics: Statics computational edition” , Soutas-Little, page 61