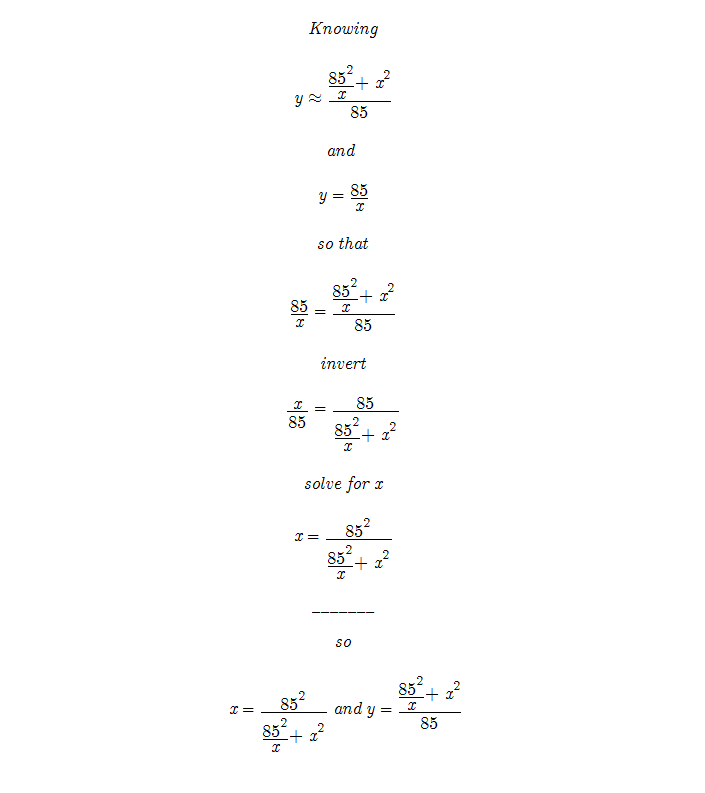

_______
Recorded 20120119
Knowing that y approx= sqrt(x^2 + y^) we know that possibly there is a trigonometric equation that will use a unique equation to solve for x only knowing x * y.
The sqrt(5^2 + 17^2) is approximately equal to 17. This means that although the numbers are small the angle between them is equal to 90 – ( 1/0.72) See Ssin and Scos.
This makes me picture a right triangle. If x and y are know we know the angle by comparing their lengths for sqrt( x^2 + y^2) and testing how far from a right triangle the answer differs.
Picture a logarithmic spiral that where every Prime number is equal to one radian as if that Prime number had been the radius of the circle. For example a radius of 3 carves out 3 radians before the radius become 5 that carves out 5 radians. It is difficult to find the change of radius; however it is valuable to picture this.
So if our Prime numbers are 5 and 17 ignore where on the logarithmic spiral they fall. Instead picture where 5 and 17 fall on a circle with radius 5 and then on a circle with radius 17. Can this be the relationship we need to find a unique equation to complete a way to find the Prime numbers that when multiplied together form a one way function? I doubt it, but this is still an important visualization.
When circles of growing radius have the same center the length covered per angle increases. Here we find the angle between 5 and 17 changes as the circle grows. However, since all circles are similar (see Curtis Blanco’s Geometry book), the larger circles are proportional to the smaller ones.
So the angle stays the same and the lengths get greater, but the arc lengths are proportional. And we can use these proportions to compare a 5 and a 17 radius triangle. The problem is doing so with both x and y unknown. The question is if knowing just the product and substituting values for x if the answer is revealed.