As you may know I believe that higher degree polynomial equations can be used to find patterns of series that would otherwise be random. I am especially interested in elliptic curves because I have read their use in cryptography. I was thinking elliptical such as ellipse, but it turns out an elliptic curve is written as y^2 = X^3 +ax + b. This turns out to be a pretty advanced concept and I am still thinking ellipse.

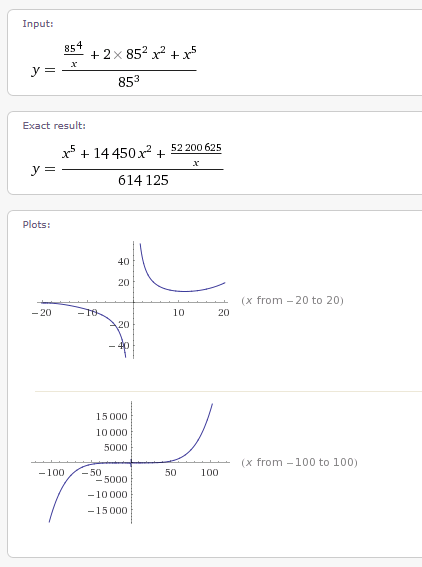
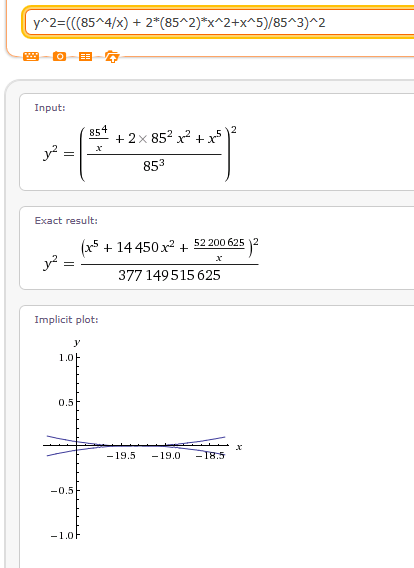
But I had a test to run. I came up with a 6th degree polynomial equation that supposedly yields the products of the 2 Prime numbers that compose 85. My test was to see if the graph had any similarities to an elliptic curve. If y^2 equals a 3rd degree polynomial and we have y = 6th degree polynomial is there any relationship between y if as y increases the square root of what y equals is in a series.

I know that is a very confusing way to look at this problem. This is just a hypothesis. I did no math other than comparing the graphs. This is all intuition. I only see a problem that might be useful if explored further.

This brings why I have posted this problem. I used Wolfram Alpha for the plot. However, once you look at the 2 plots you will see that both are mapped to x and y but do not appear to be the same graph. This may be me reading it wrong. But if I am wrong please contact me and explain. I am still learning about elliptic curves. My knowledge so far is mostly from Wikipedia. I do not fully understand, but it doesn’t make sense to only write the equation as y^2 = x^3. I know one is even power to an odd power, but that does not mean that multiples are not possible, even though they would be able to be reduced to y^2 = x^3. I am just saying that the graph should be able to be translated just as we do with curves such as the Sine curve.

This idea may be wrong. It is only a concept with no mathematical work yet. To me it is more of a way to get a better understanding of elliptic curves and elliptic curve cryptography. I want to see if there is any figuring I did that compares to ideas and structures of cryptography. It is a stretch, but my intuition tells me otherwise.