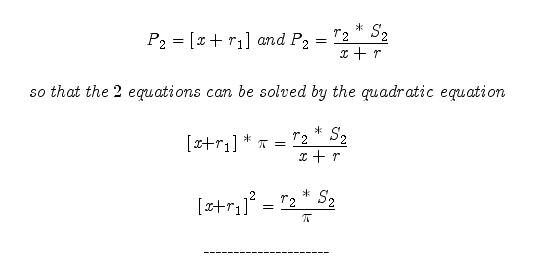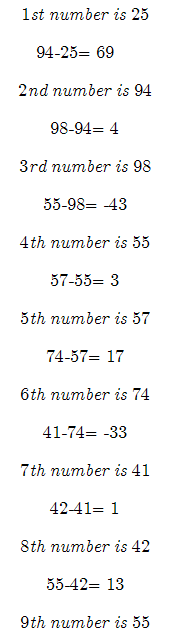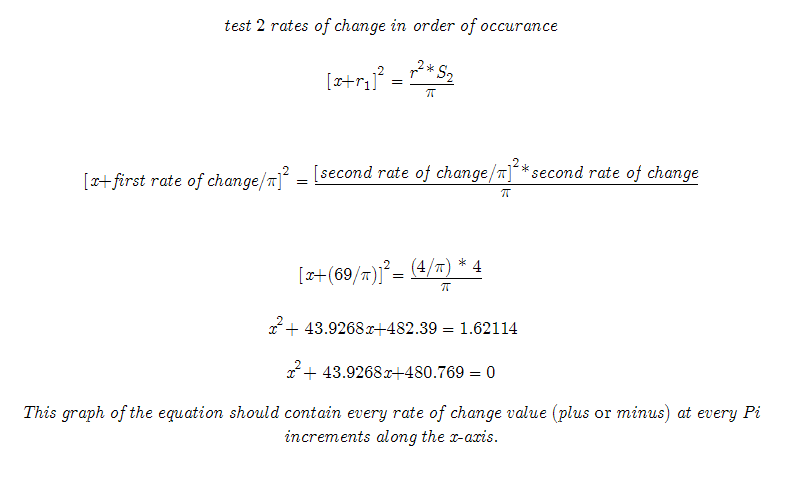Temporary Work _______ 20070916---20070919 Theory: When an equation is unknown an equivalent equation can be found if the values of the function are known and those values are in chronological order. If those values are part of function most often then the parabola found (by previous method–click here) will contain the values of all numbers of the desired function (equation). However, where the values are positioned on the parabola needs to be found. If we represent this parabola as a logarithmic spiral, in which every part of the function is mapped every Pi, we only need to solve for the equation that describes the logarithmic spiral. (Which in itself is a challenge.) Perhaps if the unknown equation’s results appear to be random, a parabola can be found between each known point and the best fit or average of the parabolas will help approximate the equation of the unknown equation. Solving for the parabola using this equation HERE. Solve for the logarithmic spiral using this experimental work. 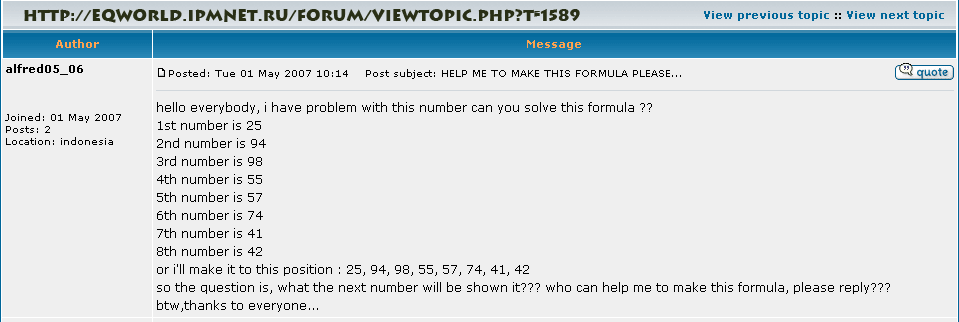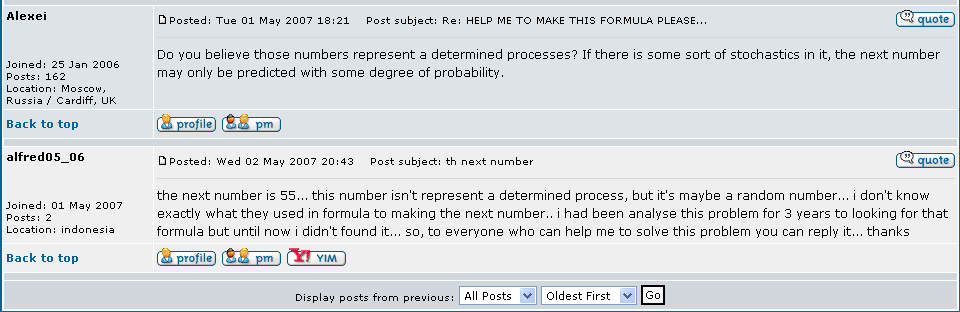(It is recommended to read all the supporting work.) Example:     Example I will used an example to a problem I found at http://eqworld.ipmnet.ru/forum/viewtopic.php?T=1589 The problem is borrowed. However the proposed solution is totally mine. That is even if it doesn’t work, it shows the concept behind how I envision these problems to work. Note we all finding a relationship between the change of the numbers. We will use the absolute value of each change. This works since the final change will be plus or minus that value. Doing so lets us find the values of negative and positive values. We are testing for a pattern in the rate of change first. That is the most logical since that is where most patterns original. However if that does not work, we will test the actual value of the numbers themselves. This graph of the equation should contain every rate of change value (plus or minus) at every Pi increments along the x-axis. It is important to note that this is just a concept. It is an idea on how to work at finding a pattern among unknown numbers that appear to be random. It would be useful in cryptography if it worked. However I am unsure of the truth of the math. It is a great concept and it is a good idea to tinker with, but the question is: Does the math hold true???   I will be adding more content to support this work soon. However do not wait and test the theory for yourself. May the Creative Force be with You!