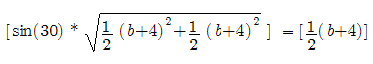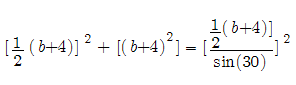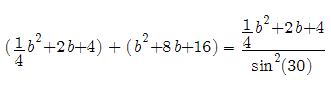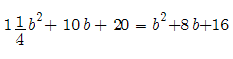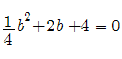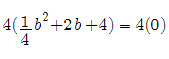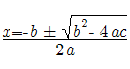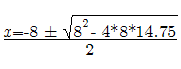Previous-------Page 1 2 3------- Next-------Math Home -------   Temporary Work _______ 20060612 It is a little confusing what exactly is trying to be solved with the “parabola key.” After all a chord can be encompassed by infinitely many circles. However what we wish to find is the circle with the correct proportions. And also, equally important is finding the first circle (smallest) that encompasses it. _______ 20060621 Let’s take a look back at how the parabola was found. It was found by basic algebra. ____________________________________ Hence with chord = 1.25 Solve for x using Quadratic Equation   x= -2.8819 or x= -5.1180 + 4 ------------------------------- 1.1180 or 1.1803 * 2 ____________________ 2.2360 or -2.2360 ____________________________________ Recall that in order to solve the “arched doorway” problem a variation of the Pythagorean Theorem was used. If this formula is used to test values of the parabola the values would be taken as the chord in the x-direction and the radius in the y-direction. This works for small values and also checks by the Pythagorean Theorem, but we know just by first observation that although both equations are satisfied, the values are too large. This leads the observer to test values with the chord in the x-direction and radius with the y-value. (Note all values are relative to the parabolas origin which is at (-4,0). So the x value would be added by 4.) Here is a random test value: a chord of 28 plugged into the equation x^2+8x+16-24 = 0 Four is added since the parabola is shifted -4 units to the left then using the Quadratic Equation to solve we get 44 or -39.1918 Here 44 is used and plugged into the Pythagorean Theorem used to solve the “arched doorway” problem First the "arched doorway" problem for reference: -2.5r = -5.5628 r = 2.22512   ____________________________________ for 44 radius and 28 chord X = 40.9878 That is the value of the length perpendicular to the bottom of the chord   It checks. And it should be the smallest circle that encompasses a chord of length 28 units!