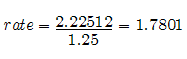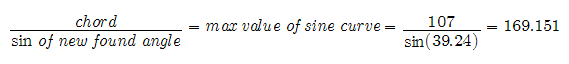|
Temporary Work _______ So far explanations have been limited to using mostly algebra and trigonometry. However, an excellent way to use the parabola that is found by chord vs. radius length is to use some things learned in calculus. So what is found by taking the derivative of a value on the parabola? _______
Ideally, if you could describe the circle over time you would have a new way to describe a parabola and ultimately the quadratic equation. (However this is based on finding a way to easily describe the circle.) Calculus has many tools to describe functions and their curves. Perhaps a new math will be developed to explain curves using circles and how much the curve deviates from the circle. The new math would be called Circulus. There is a problem with setting up a custom coordinate system or reference
circle and have it describe the curve in a useful manner. It is definitely
a challenge. But before beginning a long mathematical journey to solve the unknown and uncharted curves, perhaps something simple has been overlooked. Sometimes in math all the power of calculators and complex mathematics such as calculus are not needed. Instead a simple algebraic formula does the job. There is a simple discovery that might just prove to be the most useful application of the parabola that represents a chord. With that parabola, it is known what circle will encompass a given chord. But what if the chord lies on a circular function, such as the sine curve (or cosine) often used in the study of electricity? By knowing just the period, the cycle through which the graph makes, and the chord or value at a given x distance-- the maximum value of the circular function (also the radius of the circle) can be solved easily. _______ Theory: If an arc that encompasses a chord on a sine curve (circular function) is known, the rest of the graph can be solved, with emphasis on the maximum value. We take the parabola, (Parabola Key), and find the positive value of the radius that corresponds to the given chord. It does not matter if this is the smallest encompassing circle. However, the graph must be of a circle with constant proportion. Proportions that are based on the reference circle around the chord and are consistent throughout the parabola. (The parabola graph we use is based on a chord of 1.25 and a perpendicular bisector of 2. See Arched Door problem.) From the new radius we found on the parabola – x-chord vs. y-radius, we now have to different radius occurring at different positions. Because the change in chord is related to an involute, or unraveling string around a fixed point, (with the exception of its position not being at the center of a circle), we will assume the radius of the encompassing circle that is the max value of the sine curve occurs every Pi radians from the start of the original chord. Now we just have about enough information to solve for the max value of the sine curve. The most important factor on which all measurements are based is taking the rate of change of the chord to find the angle the new radius will be from the radius of the circle encompassing the max value of the sine curve. This rate was solved by using previous methods of solving for an unknown chord. We need to find out how much the chord changes in Pi radians. This description is hard to convey in words follow along in the example.
Attention: It is important to understand this
may not work. It is only to outline an idea and create a problem to
work on. The one main fault of this work may in fact be the rate of
the changing radius. It can be both confusing and challenging to solve.
But until these things are found work through the problem and find your
own answers. |
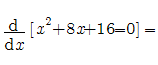 =2x+8
=2x+8