| <...Next...> | Page 1 2 | Math Home | Ideas Home |
Circle Gets a Square
A circle is usually described by its radius of arc length or rather its circumference. But what if someone took the given dimensions of a circle and describe it by a square that the circle is inscribed within? That is correct a square describes, if not defines, a circle. And that is what the challenge is: Can a square’s sides where each 4 sides equals the radius of
the circle, be found thus determining the radius and diameter of the
circle when the given information is only partially given? Specifically
if the measurements are given from a circular arc with the cord and
length the ends of the cord. (See the arc doorway problem. This is a
twist to the arc doorway problem, but the method, if discovered, would
apply to many applications and a new way to describe circles and squares.) |
Application of the Problem: The arc door problem is used here because there is already two methods (Newton’s Method and the geometry of the arc combined with the Pythagorean Theorem) by which it can be solved. Also if you can solve the square it will lead to a greater use of determining the curve on graphs. Specifically, finding out if a curve graphed f(x) is circular. Since all arcs are sums of circular arcs, you should be able to describe parts of the graph and how much the arc is from one of the circular curves. If the square could be solved it would be excellent for curve fitting computer software programs. This is no easy task and it may be impossible without the help of higher
mathematics, but I believe this problem is possible even though there
doesn’t seem to be enough measurements given. But it is necessary
to know what solving this problem means. It would give a way to find
a circle with limited measurements, but that is not the only use. As
described in the last paragraph it would be a curve fitting formula
with simple geometry. And possibly it would grant the ability to determine
how far a curve is from being a circle by comparing the rectangle created
to the square that would be formed by a circular arc.
|
Presentation of Problem: Remember this problem is without a solution and it is useful to use a circle with dimensions already know. Also note use more than one circle to make sure your assumptions work for all circles and arc lengths. Here is the problem:
|
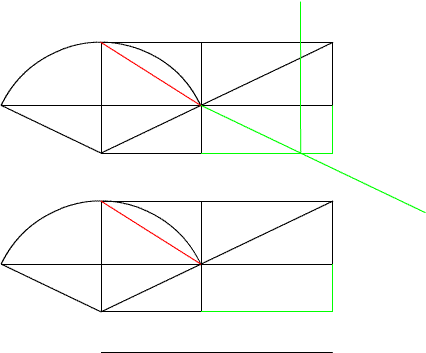
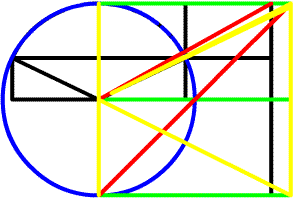
As seen here there is a circle with limited dimensions. This is a
circle arc and has methods to solve it, but here notice that this circle
is determined by a square. So the problem solver comes to the conclusion
that if the square can be solved so can the circle. Plus it has the
benefits of other solutions such as determining if an arc is circular
as mentioned earlier. Now lets us look at what we can extrude from the
given. |
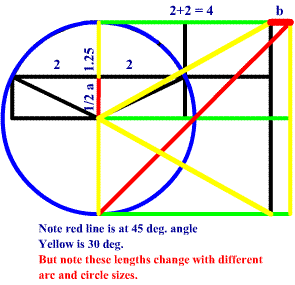
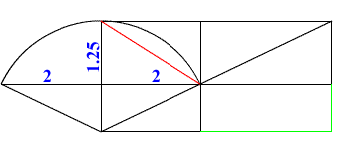
Here the radius if (½ a + 1.25) on the vertical length of
the square and (½ b + 2) on the horizontal. The diameter is (a
+ 2.5) on the vertical length and (b+4) on the horizontal. We will use these lengths as reference, but we are not limited to them. A better division of the square may be found latter. (Note if the values of a and b are substituted it just leads to a 0 = 0 equation with infinite values. You will see latter.)
|
| <...Next...> | Page 1 2 | Math Home | Ideas Home |