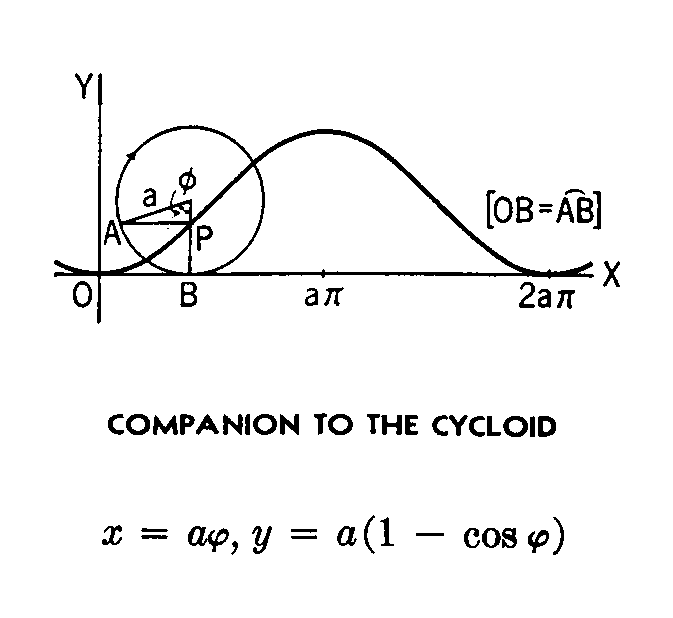| <...Next...> | Page 1 2 3 | Math Home | Ideas Home |
| Suppose you are measuring an object
that is mad of lots of curves. And you want a way to measure and evaluate
the curves. But instead of heading to the computer first you are only
armed with a set of drafting tools. You have a pair of triangles, a compass,
a circle template, and a scale. In your pocket is a Swiss Army knife and
some duct tape. And on a table in the room is some glue and some cardboard.
You mission is to measure the sine, cosine, and tangent of any point that is on the object made of curves. What we need is a starting point. What if we were to wrap a function across another function? In this case we have a circle and there are many circular functions. Perhaps is we were to roll the circle along the curves of the object, it would describe the curves. In other words, we will roll the circle like a wheel along the road of the curves of the object. A circle is based on trigonometric functions. In fact one of the equations
describing the circle is So the plan is to use a circle ( which is moving like a wheel) to find
the value of the sine and cosine of the curve. The first step is to
find how a circle moves across a horizontal line. The curve that is
formed is called the cycloid (ordinary case). |
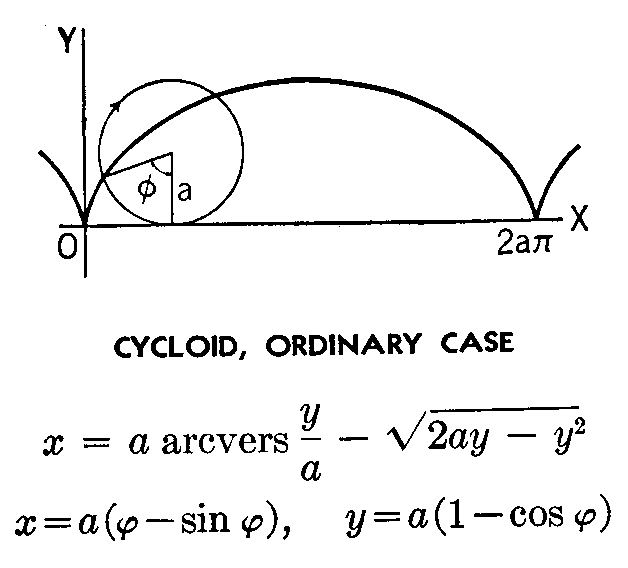 |
| Well that gives us a curve that can be put
into equation form, but the equation if difficult to work with. (it is
difficult to work with but it may have use for something) But we are looking
to draw the sin and cos out of a circle in motion. And then use those
values to find the tangent. The trigonometric values will probably prove
to be the most useful when describing the objects curves.
But there are variations to the cycloid. One being the companion to
the cycloid. It is useful because the curve it creates is already like
the sine and cosine. It is just out of phase. |
|
| <...Next...> | Page 1 2 3 | Math Home | Ideas Home |