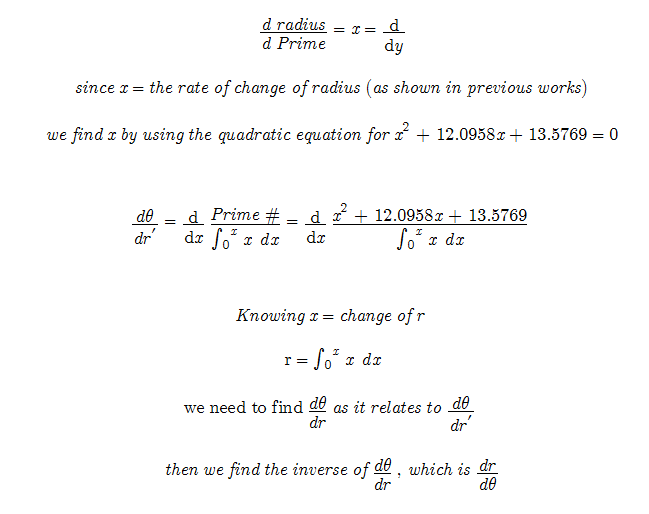_______ 20080213 from 20080127 Before Newton invented the laws of motion, mathematicians and especially ordinary folk had a “feel” for what now is easily expressed by a set of equations. This feeling was based on personal experience and observation. The user knew what they were looking for, they just couldn’t explain it simply. This is true and shown today in geometry and every skill. It is true when us would be mathematicians (including those who don’t know they are mathematicians) try and solve an unknown or new math problem. This mean that sometimes you get ideas that don’t seem worth pursuing. It seems too abstract or to difficult to describe in a simple sentence. How do you decide if it is worth pursuing? This is were math, a logical field, becomes an art form: You have to go by “feel”. Often, the answer doesn’t come easy. (Or else someone would have already discovered it.) It is also a question of effort. How long do you want to spend figuring and testing ideas? But even with a little effort something is learned. And your one step closer to discovery. You can’t measure the distance between success and failure, because the road is not linear. Likewise, the closeness to discovery could be an equation or rely on several future discoveries.   That is where this logarithmic spiral vs. Prime numbers begins. I have been trying to solve this for almost a year. It is thought that Primes have no pattern. But the benefits to their discovery are huge. I have tried with 2 different spirals and failed. However, I still believe that a spiral can find the pattern between many series including Primes. After all if the modulus can be described as values wrapping around a circle, isn’t a logarithmic spiral just a continuation of that concept? 1 However my latest attempt has 3 main characteristics that is must met if it is going to work. It will be helpful to read the previous post Here There is some corrections.   Summary: This remains untested which means there is a great chance that it is wrong. However the idea is outlined here. If the idea is correct all that needs to be found is the inverse of the derivative for d-theta / d radius . This is just a draft. I will try to develop the ideas further. But until then... May the Creative Force be with You References: 1. "The Code Book" , Simon Singh ------- Hopefully it is clear what is being attempted to be solved here. I will post updates to better explain and hopefully solve this problem. This is a good group project. If you have read this and want to work on a problem email: trurlthe_constructor@hotmail.com . Also more math can be found in the math_hunches section of Constructor’s Corner.