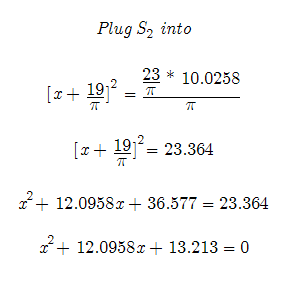|
Temporary Work _______ Before reading review previous work. So far it has appeared as if my work on Prime numbers related to a logarithmic spiral has proved nothing. But nothing could be further from the truth. Sometimes even if you put a lot of effort into a problem an it isn’t solved, new ideas and hypothesis are formed. Here at Constructor’s Corner we call them “hunches.” And it is true that other times you have a hunch and you know the information is groundbreaking, but it just seems that figuring the solution to problem is impossible. Long story short: My first attempts had many errors. And much of it proved to be untrue. But underneath it all I had a hunch and it still is a hunch. The solution relies on the “boxed” logarithmic spiral where [chord = Prime # / Pi] and [ r = # / Pi] being a true logarithmic spiral or at least an approximate logarithmic spiral. What I am about to show will prove or disprove this hunch. To start it must be stated that the assumed log spiral of [S = Prime #] is not a true logarithmic spiral. It is just a spiral that has no clearly seen harmony. However it is still may have some use. In fact, the same equations we used trying to find the equation for this spiral may be used on the “boxed” logarithmic spiral. Assuming that the boxed spiral is a true logarithmic spiral. I see 2 ways to solved for its equation: 1. Find a involute which intersects its values. An involute will be a boxed logarithmic spiral that is perfectly square and whose values occur at 45 degree angles. If that unique involute can be found its equation and values can be put into the log spiral equation. 2. We can find a quadratic equation that describes the boxed logarithmic spiral. If it can be found the equations we get from the parabola will help us solve the log spirals equation and find the values of a and b. (This will be our approach. I have tried it before, but the [S = Prime #] proved not to be a true log spiral.)
We know have a quadratic formula that we can use to get values from the parabola. Ironically it is very similar to the previous parabola solved previously. This is not what I was expecting. I was expecting a whole new quadratic equation. That means if the math on the previous work holds true we could solve for a and b in the logarithmic spiral equation. We would have the problem of not knowing the angle at which the Prime numbers occur. However the boxed spiral’s lines intersect the log spiral itself. Restated, using geometry we can find the angle (theta). We can try solving for its values. If the math doesn’t break any rules and it does not give us a value, we must determine if the boxed spiral is in fact a logarithmic spiral. May the Creative Force be with You ------- Hopefully it is clear what is being attempted to be solved here. I will post updates to better explain and hopefully solve this problem. This is a good group project. If you have read this and want to work on a problem email: trurlthe_constructor@hotmail.com . Also more math can be found in the math_hunches section of Constructor’s Corner. |