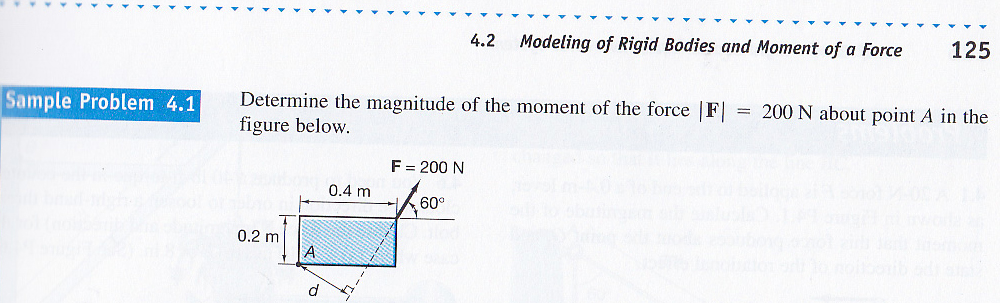
20100811---0909
There are 4 ways of solving this problem. One vector and three different trigonometric approaches that have the same result. I will show my way. Not because it is better, but because of the interesting reasoning behind it.
Imagine the entire rectangular body of the rectangle shape in this problem rotated around a fixed axis where the 200 N force occurred. To find the side adjacent (the line of action) to side d (the length of the arm) we imagine the diagonal of the rectangle rotating around the upper right point (where F occurs) and find the length that would by orthogonal by multiplying "the line or action" by the sin(60). That's it!
What just occurred here? Do you recall the arched doorway problem previously on constructorscorner.net? It applies here, but we don't need it. The diagonal of the rectangle will trace our a circle. It is the radius of that circle. The sine of the angle of rotation (60 degrees in this example) is how much shorter it would have to be to the orthogonal of its previous location.
What is the application? It simplifies some calculations. But the real beauty is the application of how many, different, multiple, or different angles effect the static equilibrium.
Sin (60) * diagonal of rectangle = 0.387299 (our observation)
x^2 = sqrt (d^2 + 0.387299^2) (Pythagorean Theorem)
x = 0.372815
approximately equal to 0.387299