Arcs and Area Solved Page 01

<...Previous...>

<...Next...>

Page 1 2 3 4 5 6

Math Home

Ideas Home

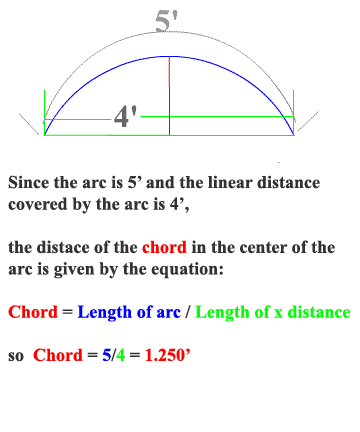This is a new look at the same arched door. First we will find the chord that is in the center of the doorway.

But know it is important to look at the given and find those clues that we may not notice at first glance.

Now direct your attention to known lengths that we have solved underneath the arc.

Refer to the next picture below.

Now we have sides of the right triangle. But this is not the angle that we are concerned with.

Look at the radius that is at pi/2 and the radius that is at the right of it that is at an unknown angle we must find.

Here is what we know:

As the cos of the angle (between the two radius) moves 2 feet it makes and arc of 2.5 feet. At this time the sin of this angle with radius r moves 1.25 feet.

So the two lengths that we have found in this picture show how much the sine and cosine have change between these two radius.

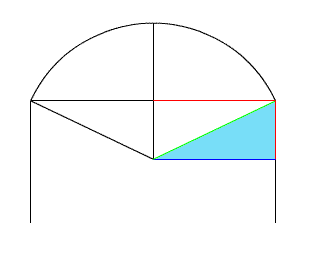Let us look at the drawing drawn to scale. We can see the triangle (highlighted in blue) that is formed by the values we just found from the chord and the given 2 foot x segment.

Try to picture in your mind what makes this triangle and the value of its sides so special.

As you can see in the next example these values can be used in the Pythagorean Theorem to solve for r :) !!!!!!!!

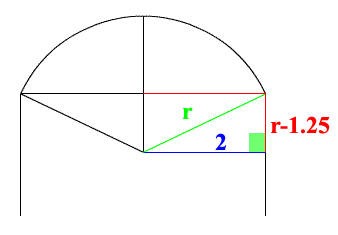Here are the values. The value of 2 is the hardest if possible to find. Luckly it was given in the problem by 4/2.

See if you can now solve for r.

Page 1 2 3 4 5 6