_______
20100425---0426

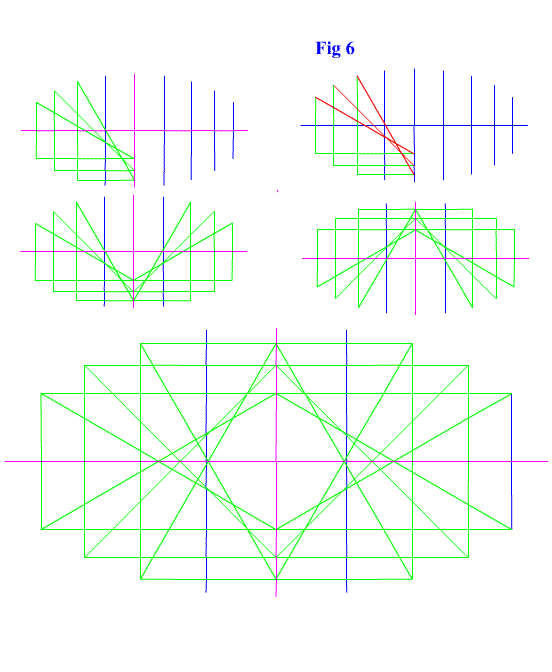
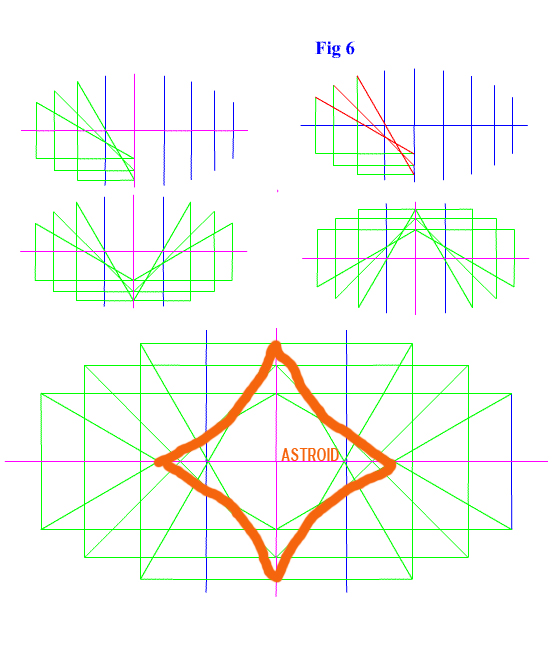
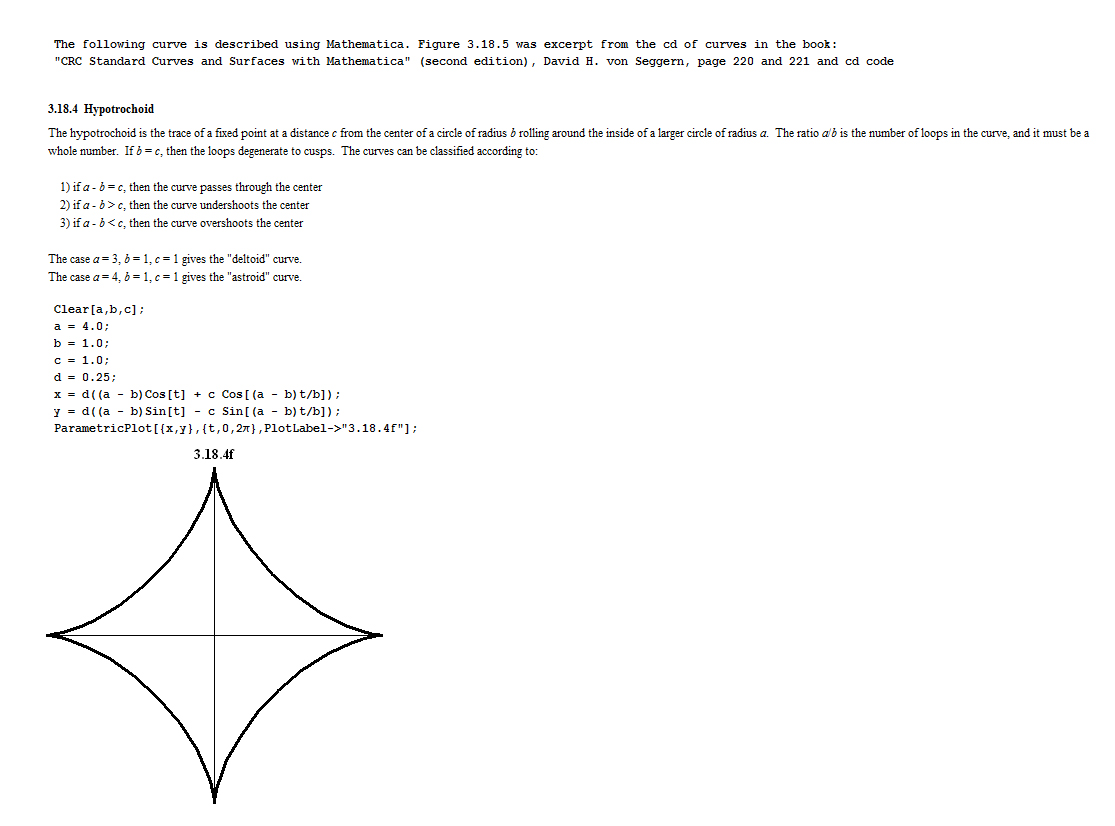
So why have I shown this curve excerpted from the book. It is because of a simple observation that I made comparing an ellipse to this astroid. In a problem from several years ago I drew and ellipse composed to right triangle and a radius. It was nothing groundbreaking, just a simple observation. Now I was working with ways to use a right triangle and ellipses to describe curves. I believe there are many curves that can be solved this way. This is especially interesting with 3D shapes. In the center of the ellipse I drew is a 2D and 3D astroid. Note that although the angle is formed by a series of lines there is a curvature. That is the slope of the sides are not triangles---the triangle are just to certain points on the curve. (At least I hope.) If you were to rotate this shapes area around the x or y axis using calculus, a 3D astroid would be produced. But the exciting part is this is only a geometric observation. If we can find this shape in an ellipse what other shapes can we describe with equations we already know?

Look at the following pictures and link to review the ellipse drawing. Click Here for ellipse write-up.