Extraordinary Ellipse Page 02

<...Previous...>

<...Next...>

Page 1 2 3

Math Home

Ideas Home

Start by drawing the beginning of a circle with the cosine being the distance in the x direction and the sine being the height in the y direction. Draw only in the first and second quadrant. The lines should be drawn upwards. See figure 2.

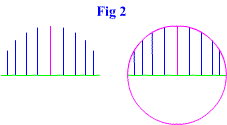We just drew a circle for reference. Now draw a line 2 units along the coordinate plane and place its center at zero. From here draw the cosine and sine distance again but keep the lines centered vertically along the 2 unit long line. Restated, put the lines at a distance of the half the sine above the original 2 unit line and half the sine below the 2 unit line. Do this while maintaining the distance of the cosine in the x direction. See figure 3.

Now look at what you just drew. It has an x distance of the cosine and a y distance of half the sine. But it is also the structure behind an ellipse! And not just any ellipse. This ellipse describes the sine, cosine, and tangent. And with a little more investigating we see that it is the structure of the ellipse is a segment of the length of one. This is a similarity it shares with the unit circle. See figure 4 and figure 5.

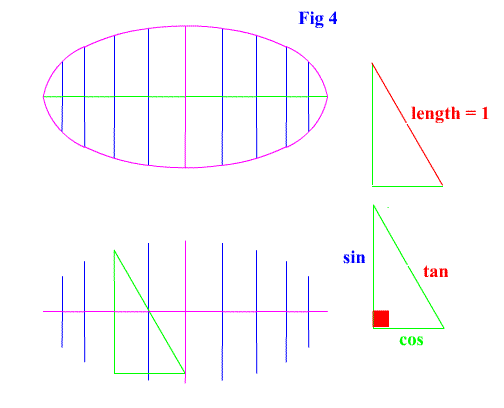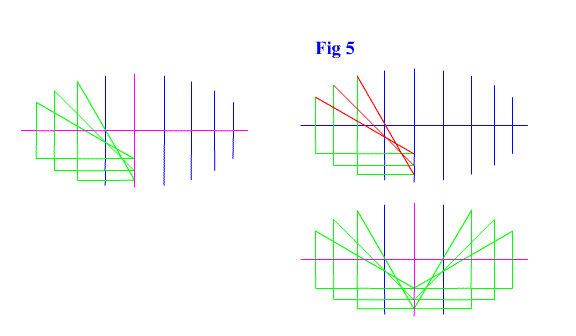So we have just found that a bunch of triangles (triangles that are formed by the sine and cosine) can be placed to form and mathematically describe an ellipse. See figure 6 for the equation of an ellipse

The triangles define the ellipse. The hypotenuse of those triangles has a value of 1. With the cosine in the x axis and the sine centered along the y axis the line will continue to rise up the minor axis until it reaches the top to the line (in 1- sin/2 increments).

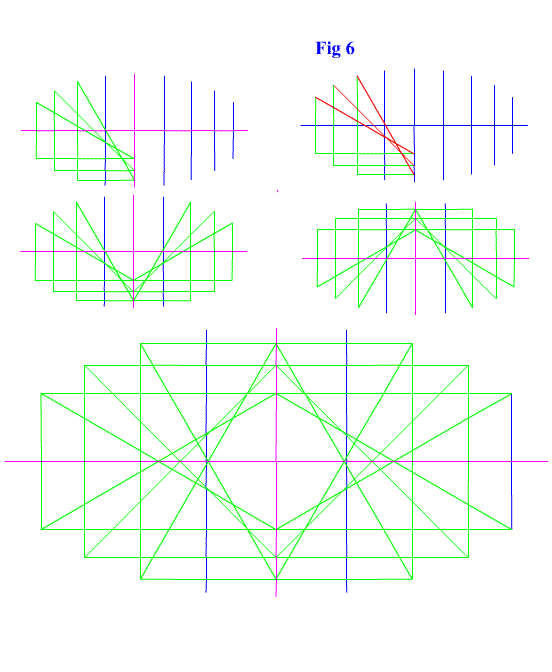The triangles form the orbitals of the ellipse. As figure 6 shows, drawing the triangles from one end of the minor axis to the center of the minor axis is enough to complete the ellipse. It makes an awesome and complex shape.

Page 1 2 3