| <...Previous...> | <...Next...> | Page 1 2 3 4 5 6 | Math Home | Ideas Home |
If we take a look at how the arc doorway problem was solved be just using elementary mathematics (below calculus). Basically we are solving for two lengths. One is the with of the height of the arc in the center from the base at each ends. And the other length is the length between the two arc ends.
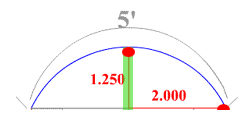 |
But the fact that all three segments are all radiuses that meet at the same
center point we are able to determine variables for the sides. Since the middle
length is known (1.25), we know that the length of one of the sides of the right
triangle is r-height of arc from arc ends or r-1.25 in this problem. And the
length from the end of the arc to the bottom center of the arc is given as 2
in this problem. We then know the third side is one of the radius and is the
unknown in this equation. Thus we can use the Pythagorean theorem we can solve
for the equation:
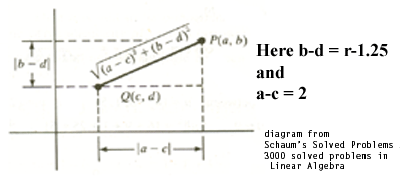 |
 |
What have we just solved here? It is so simple once you see it. The solution uses the Pythagorean and a form of simple addition and subtraction along the coordinate plane.
But what about those three radius. Is there anything more to discover with them.
We took information about those three radiuses without knowing their values
and used the two lengths of the arc to find the value of the radiuses. And once
you know the radius you can find many things about a circle. But those three
radiuses not only find the value of the radius it determines the whole arc.
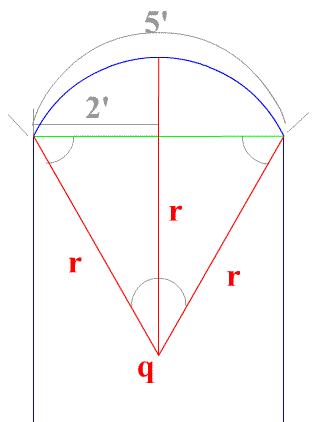 |
We can describe the circular arc using just three radiuses. Since the arc is symmetric in length and shape (and it is a circular arc) it can be described by use of an isosceles triangle! The sides being of equal length and a base that equal the radius minus the height of the center arc length. And base plus the height of the center arc is equal to the sides (other radiuses) of the isosceles triangle.
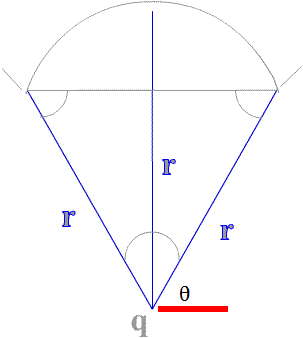 |
Here are three radius in an isosceles triangle. These three lenghts determine the size and shape of the circular arc above. Here the two sides equal to the radius of the arc and the base plus the segment equals the radius so:
|
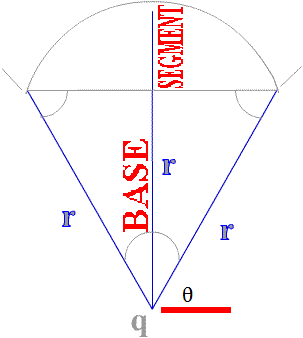 |
A circle is really made up of many isosceles triangles. The are used every time
that you solve a length on the unit circle. And it may be of use in the future
to see how these isosceles triangle relate to the unit circle and also how the
height and width of the arc segments compare to the radius.
This should be explored further.
| <...Previous...> | <...Next...> | Page 1 2 3 4 5 6 | Math Home | Ideas Home |
