| <...Next...> | Page 1 2 3 | Math Home | Ideas Home |
Extraordinary Ellipse
We are already familiar with the “unit circle.” We have already used it to define circular functions such as the graph of the sine or cosine. We also know from algebra that a circle is a conic section. Picture two cones with their points facing each other. A circle is formed by slicing the cone with a plane that is perpendicular to the cones. See figure 1. |
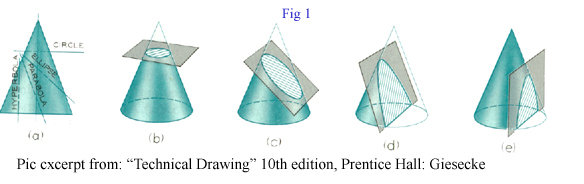
But what if we could describe some of the other conic sections using the sin or cosine or convert the unit circle to match the properties of the new shape. We will be describing the ellipse using the sine and cosine. It is
another conic section that is formed by using a cutting plane at an
angle to one of the cones discussed earlier. See figure 1. |
The idea to describe an ellipse by the sine and cosine comes from my work with vectors. I believe that ellipses and circles can be used to find many things with problems dealing with velocities, rotation, and forces. In fact, ellipses and circles are already used all the time to explain and solve these problems. But perhaps there exists an approach to solve such problems that was hidden in plain sight. Before the equation is given we are going to draw the ellipse.
|
| <...Next...> | Page 1 2 3 | Math Home | Ideas Home |