| <...Previous...> | Page 1 2 3 | Math Home | Ideas Home |
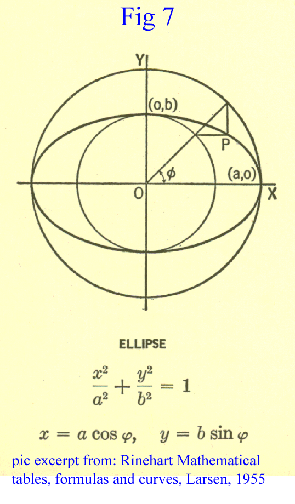 |
|
|
Figure 8 explains the length that was solved for in the previous equations. The length is in blue and 1/2 sin is in the bold magenta. This equation is similar if the sine is graphed in the x axis and the cosine is the y axis. Everything is done in almost the same way, but instead of the slope of the trianges formed being the tangent, it is the cotangent. |
 |
Figure 9 shows where the focus occurs. In this example (cos vs sin) it occurs at cos(30) * 1 and cos(30) * -1. |
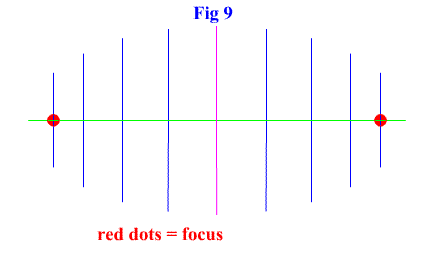 |
So now we have an ellipse that has similiar properties to that of a unit circle. (In having a way of describing the sine, cosine, and tangen.) But as we have seen this is an extremely extraordinary ellipse. It explains the sine, cosine, and tangent. But the wonder is in where the equation and shape fit the requirements to form an ellipse. It is important to note that this equation and shape does not explain every single ellipse in the way that the unit circle explains all circles. This is a special ellipse and it might hold many uses to explain things the way the sine and cosine do, but ellipses consist of many different shapes and sizes unlike circles. But the ellipse does have possible other applications and is unique enough to be worth studying. |
For now have fun finding applications and problems where this ellipse belongs. And as alway feel free to post messages on the message board. |
| <...Previous...> | Page 1 2 3 | Math Home | Ideas Home |
