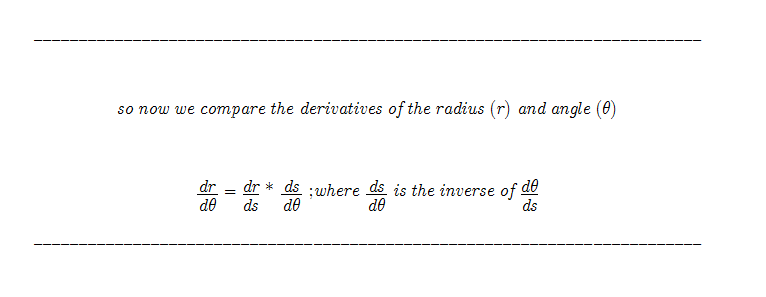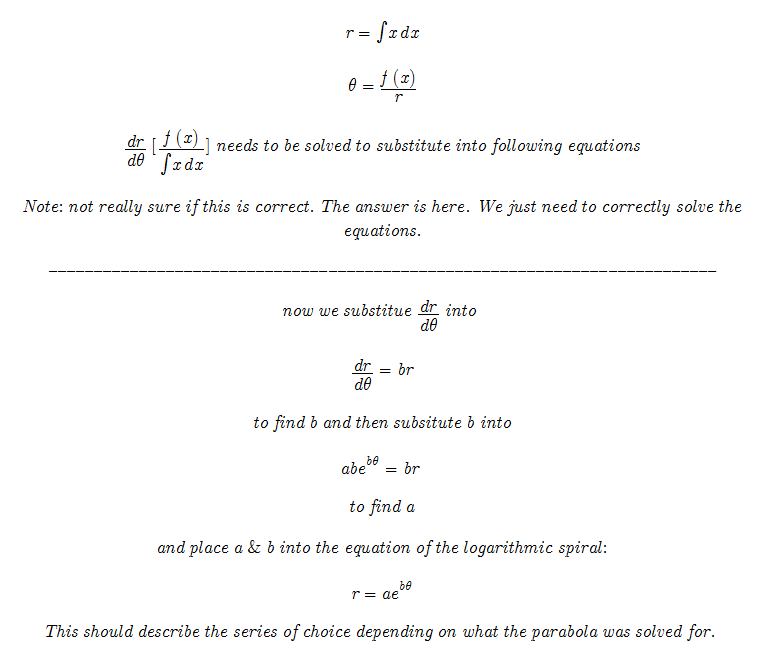|
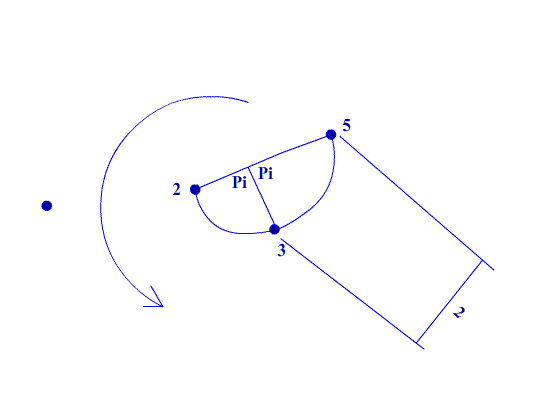
Temporary Work _______ The Chord vs Circular Function was very interesting, but a very difficult challenge of finding the rate of change of the logarithmic spiral occurs. It may be possible, but other approaches to the problem may prove easier. My original equation and the parabola that was found was correct. We have already seen that the equation is always true for a given value. That is fine. We have found “x” in the Corrected Solution. The pattern of Primes occurs on how the numbers fit across the logarithmic spiral. That is a Prime number occurring in sequence every Pi radians. I drew a spiral that tried to show this. The spiral was not a logarithmic spiral, but it also wasn’t a true representation of the equation or the parabola. I tried to use circular arcs to draw the logarithmic spiral. It didn’t work. It is very difficult to draw, but I will try to show in sketches how the logarithmic spiral is formed.
Basically at every Pi radians (the angle between Prime values), the next Prime occurs. It can be very hard to determine using already known equations of a logarithmic spiral. I tried to draw it with circular arcs but did not succeed. It is very difficult to describe non-circular curves mathematically. But with previous attempts of Spiral Encryption, we should have the tools to solve the spiral. It is a conundrum without the Spiral Encryption tools. We know 2 points and the change of radius; the total arc length from the center of spiral; and lastly the angle of Pi radians. That should be enough to define the spiral, but a new way of describing logarithmic spirals would have to be invented. That is why we turn to the easier (relatively) Spiral Encryption. Another error in the previous Spiral Encryption is that I used the wrong “x”. In the Corrected Solution we found the correct value of x and y. Substituting these correct values into the Spiral Encryption work we may find a solution that describes the logarithmic spiral and thus Prime numbers. Test it for yourself! Of course there might be slight mathematical errors but the overall concept is here. Below is a copy of Spiral Encryption. I have made corrections
These pictures are separated because this is the difficult part I am unsure of. The goal is to find the [derivative of the radius R] as opposed to [the angle]. There will most definitely be errors here.
May the Creative Force be with You ------- Hopefully it is clear what is being attempted to be solved here. I will post updates to better explain and hopefully solve this problem. This is a good group project. If you have read this and want to work on a problem email: trurlthe_constructor@hotmail.com . Also more math can be found in the math_hunches section of Constructor’s Corner. |