|
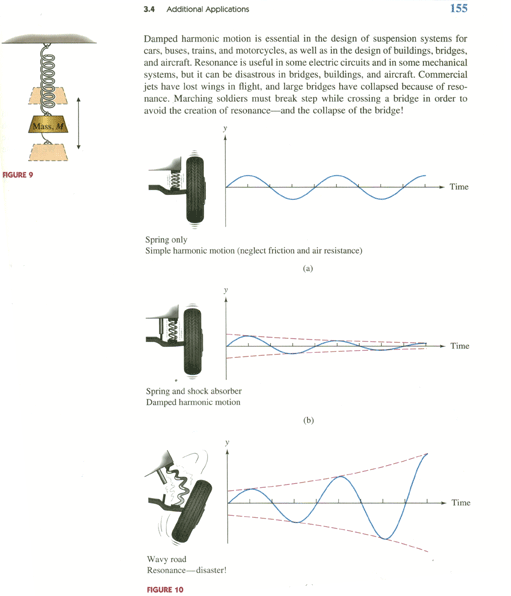
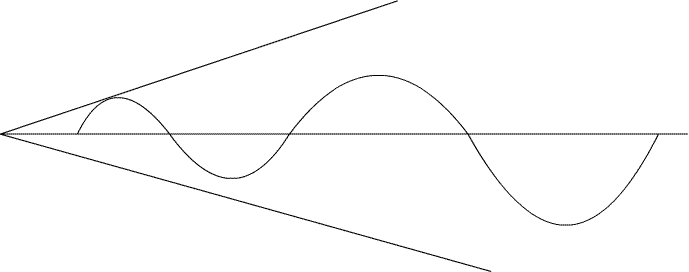
Temporary Work _______ I am going to “wrap up” work on Prime numbers soon. It has been over a year since I started and I only have some creative ideas without solid results. But that’s how it is with Primes. That doesn’t mean I will completely give up. I will continue to work on Primes, but focus more on other subjects and other projects. But why not try one more idea that doesn’t work? There is also a question of when to conclude work on a math problem. It is when you are out of definable “hunches”. I don’t have anything that I is complete and can be written about in a clear manner. But that doesn’t mean another future hunch won’t bring a breakthrough. Onto the idea that doesn’t quite work: So far the theory that many series including Prime numbers can be represent by a involute and logarithmic spiral has been established. However finding that specific spiral that defines Prime numbers is no easy task. However we have something to work with. In previous work a parabola was found by the equations that are described by Prime numbers. In another working theory it is stated that a parabola can be translated into a involute or logarithmic spiral. The only questions are how to derive this spiral from the parabola, and once derived, does it explain the pattern and predictability of Prime numbers? Resonance: My definition of resonance after reading the following excerpted page is: “force that is lessened by an object over time; however there is not enough time to dampen the force before another force is applied”. Not an exact definition but you get the idea. It is often in mechanical and electric disciplines. But I’m going to apply it to an involute. That is starting with the parabola from which the involute is derived. *the following diagram is except from "Analytic Trigonometry", Barnett and Ziegler 6th Edition Log Spiral Shifted by Sine Wave or Line: *the following spiral is a log spiral with "shifted values" in an attempt to find a true log spiral; S=Prime
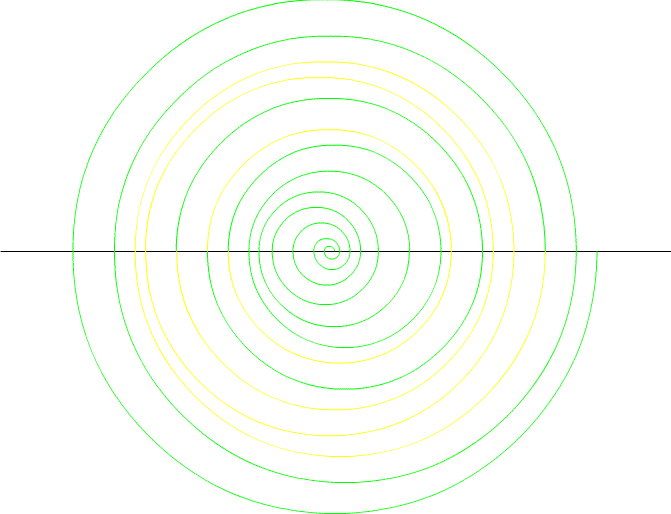
*here is the same spiral--in the small values it appears to be a true log spiral; S=Prime
*below is the boxed spiral--it looks like a spider web--may help lead to a true log spiral
Involute: The theory is that all parabolas can be represented by involutes. However it is difficult to find the rate of change. Sine Curve Effected by Resonance Creating Involute: If you view the values of a parabola as they relate to a circular function such as a sine curve, as the parabola increases it is as if the sine curve is affected by resonance. The value of the sine curve is the absolute value of its change from the last value. In other words, the rate of change of the sine curve equals that of the parabola.
_______ As seen in the Chord vs Circular Function it is explained how a sine curve fits a parabola. The exact proportions of the chord to the radius may not be correct. But this is only to express an idea. The theory from the Chord vs Circular Function is: “Theory: If an arc that encompasses a chord on a sine curve (circular function) is known, the rest of the graph can be solved, with emphasis on the maximum value. We take the parabola, (Parabola Key), and find the positive value of the radius that corresponds to the given chord. It does not matter if this is the smallest encompassing circle. However, the graph must be of a circle with constant proportion. Proportions that are based on the reference circle around the chord and are consistent throughout the parabola. (The parabola graph we use is based on a chord of 1.25 and a perpendicular bisector of 2." See Arched Door Problem So if we can determine the correct rate of change, we can determine a pattern between the x chord and y radius because of similar proportions between circles. Chord on Sine Curve Increasing Proportional to Certain Chord vs Radius: Theory: The rate of a parabola can be determined by the proportion between the chord and radius. This means that a pattern should occur at similar proportioned circles. This needs to be investigated further. There is also a problem of the equations being always true having a correct value at every number. That happened with the parabola of the Prime Numbers. However moving a distance of every Pi along the graph of the parabola may reveal a pattern. Derivative or Rate of Change of Parabola: *here is the derivative of the parabola that was solved before
The derivative doesn’t seem to show much but it may lead to the clues that determine the rate of change of the involute. Conclusion: I realize it is hard to see the goal of the following work. It might even turn out to be untrue. But it remains my best “hunch” to finding any predictable pattern or any pattern at all between Primes. The work doesn’t stop here. This is just a start. However I will be also working on different problems while I continue the Prime work. I also will turn to work that has already been found, such as textbooks on Primes. But remember, even if the work proves untrue, there is still much to be learned here. Admittedly this writeup is confusing, but it will begin to make sense with following writeups. The drawings are big placed in the web page because I wanted to show the pattern in detail. Download the Flash picture: log_spiderweb This is just a quick draft to show the concept.
May the Creative Force be with You ------- Hopefully it is clear what is being attempted to be solved here. I will post updates to better explain and hopefully solve this problem. This is a good group project. If you have read this and want to work on a problem email: trurlthe_constructor@hotmail.com . Also more math can be found in the math_hunches section of Constructor’s Corner. |